Slide transcript

Slide transcript#

I am working on finding ways to increase accessibility of the beamer slides provided. The following is an automatically generated transcript from the pdf of the slides but is still not perfect. I would be happy to hear feedback on how this transcript can be improved for additional usefulness.

Lecture 6 - Here Comes the Homology#

Goals#

Goals for today:

Homology!

More on the boundary map#

$p$-Chains#

Let $K$ be a simplicial complex and fix a dimension $p$.

A $p$-chain is a formal sum of $p$-simplices in $K$, written

\[\alpha = \sum a_i \sigma_i\]
$p$-chains are added component-wise: if $\alpha = \sum a_i \sigma_i$ and $\beta = \sum b_i \sigma_i$, then $\alpha + \beta = \sum (a_i + b_i) \sigma_i$
The collection of $p$-chains with addition is called the $p^\text{th}$-chain group (vector space), $C_p(K)$.

Boundary maps#

\[\begin{matrix} \partial _p: & C_p(K) & \to & C_{p-1}(K)\ & \sigma = [v_0,\cdots,v_p] & \mapsto & \sum_{j=0}^p[v_0,\cdots,\widehat{v_j}, \cdots v_p] \end{matrix}\]

Matrix representation#

$\partial_1(K) =$

	AC	AD	AE	BE	CD	CE	DE
A
B
C
D
E

Chain complex#

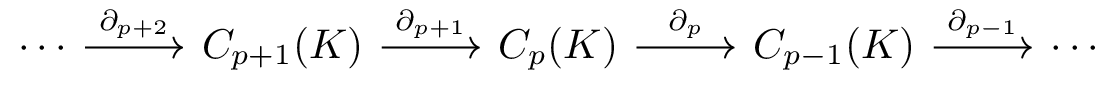
chain complex

\[\begin{matrix} \partial _p: & C_p(K) & \to & C_{p-1}(K)\ & \sigma = [v_0,\cdots,v_p] & \mapsto & \sum_{j=0}^p[v_0,\cdots,\widehat{v_j}, \cdots v_p] \end{matrix}\]

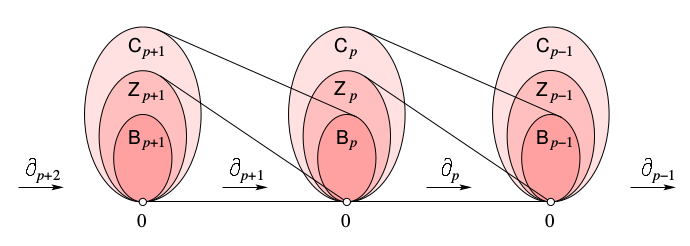
Cycles and Boundaries#

Important subspaces for a linear transformation#

Image
Kernel

Cycles#

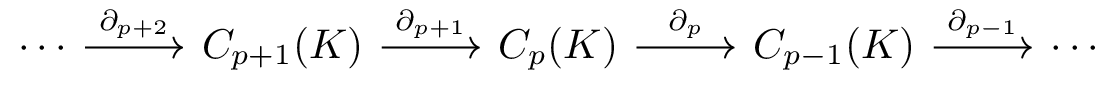
A chain in the kernel of $\partial_p$ is called a $p$-cycle. chain complex

The collection of $p$-cycles forms a subspace $Z_p(K) \subseteq C_p(K)$.

What is a 2-cycle?#

More work space if needed#

Boundaries#

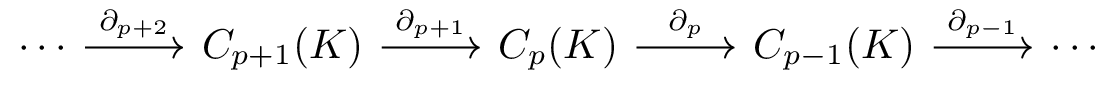
A chain in the image of $\partial_{p+1}$ is called a $p$-boundary. chain complex

The collection of $p$-boundaries forms a subspace $B_p(K) \subseteq C_p(K)$.

Nifty trick#

Theorem#

$\partial_p\partial_{p+1}(\alpha) = 0$ for every $(p+1)$-chain $\alpha$.

Translation#

Every $p$-boundary is a $p$-cycle.

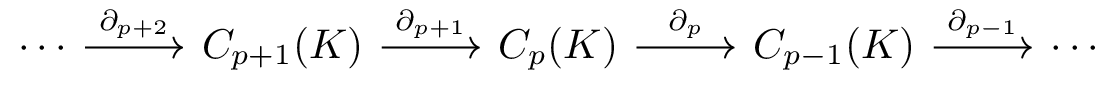
Chain complex

$B_p(K) \subseteq Z_p(K) \subseteq C_p(K)$

Try it: Cycles and boundaries#

What are the generators of $B_1(K)$? Of $Z_1(K)$?

Try it: Cycles and boundaries#

What are the generators of $B_1(K)$? Of $Z_1(K)$?

Try it: Cycles and boundaries#

What are the generators of $B_1(K)$? Of $Z_1(K)$?

Homework (In case we only get this far)

DW 2.6.3) Let $K$ be the simplicial complex of a tetrahedron. Write a basis for the chain groups $C_1$ and $C_2$; boundary groups $B_1$ and $B_2$; and cycle groups $Z_1$ and $Z_2$. Write the boundary matrix representing the boundary operator $\partial_2$ with rows and columns representing bases of $C_1$ and $C_2$ respectively.

Homology for real now#

Quotient space#

Let $V$ be a vector space over a field $k$. Let $W \subset V$ be a subspace. Define $\sim$ on $V$ by $x \sim y$ iff $x-y \in W$.

The equivalence class of $x$ is denoted $$[x] = x + W = \{x + w : w \in W\}.$$

The quotient space $V/W$ is then defined as $\{[x] \mid x \in V\}$. This is also a vector space with:

Scalar multiplication:
Addition:

Homology#

Definition: The $p^{\text{th}}$ homology group is the quotient space $$H_p(K) := Z_p(K)/B_p(K)$$

Slide transcript

Contents

Slide transcript#

Lecture 6 - Here Comes the Homology#

Goals#

More on the boundary map#

\(p\)-Chains#

Boundary maps#

Matrix representation#

Chain complex#

Cycles and Boundaries#

Important subspaces for a linear transformation#

Cycles#

What is a 2-cycle?#

More work space if needed#

Boundaries#

Nifty trick#

Theorem#

Translation#

Try it: Cycles and boundaries#

Try it: Cycles and boundaries#

Try it: Cycles and boundaries#

Homology for real now#

Quotient space#

Homology#

Tryit: What is \(H_1(K)\)?#

Tryit: What is \(H_1(K)\)?#

Tryit: What is \(H_2(K)\)?#