Slide transcript

I am working on finding ways to increase accessibility of the beamer slides provided. The following is an automatically generated transcript from the pdf of the slides but is still not perfect. I would be happy to hear feedback on how this transcript can be improved for additional usefulness.

Lecture 4 - Nerve, Cech, and Rips Complexes

Section 2.2 Goals

Goals for today:

• Complexes from point clouds: Rips & complexes

• Sparse Complexes: Alpha complex Recall: Geometric vs Abstract Simplicial Complex

• Given a collection of points \(V \subseteq \mathbb{R}^N\)

• For a subset of these \(\{a_0,\ldots,a_n\}\), a (geometric) \(n\)-simplex is the convex hull of the points.

• A simplicial complex is a collection of geometric \(n\) simplices so that

  • Every face of a simplex is also in the complex.

  • The intersection of any two simplices is either empty or a face of both.

• Given a finite set \(V\)

• An abstract simplex is a subset of \(V\).

• An abstract simplicial complex is a set \(K\) of finite subsets of some \(V\) such that if \(\sigma \in K\) and \(\tau \subseteq \sigma\), then \(\tau \in K\).

and Rips Complexes

Point cloud

A point cloud is a (finite) collection of points in a metric space \((M,d)\).

Ball

\[B_o(x,r) = \{y \in M \mid d(x,y) < r\}\]

\[B(x,r) = \{y \in M \mid d(x,y) \leq r\}\]

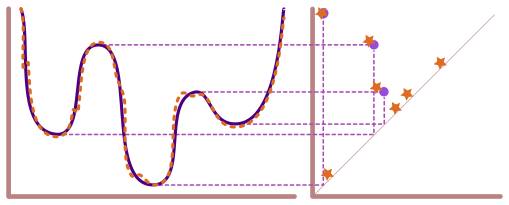
What we want to study

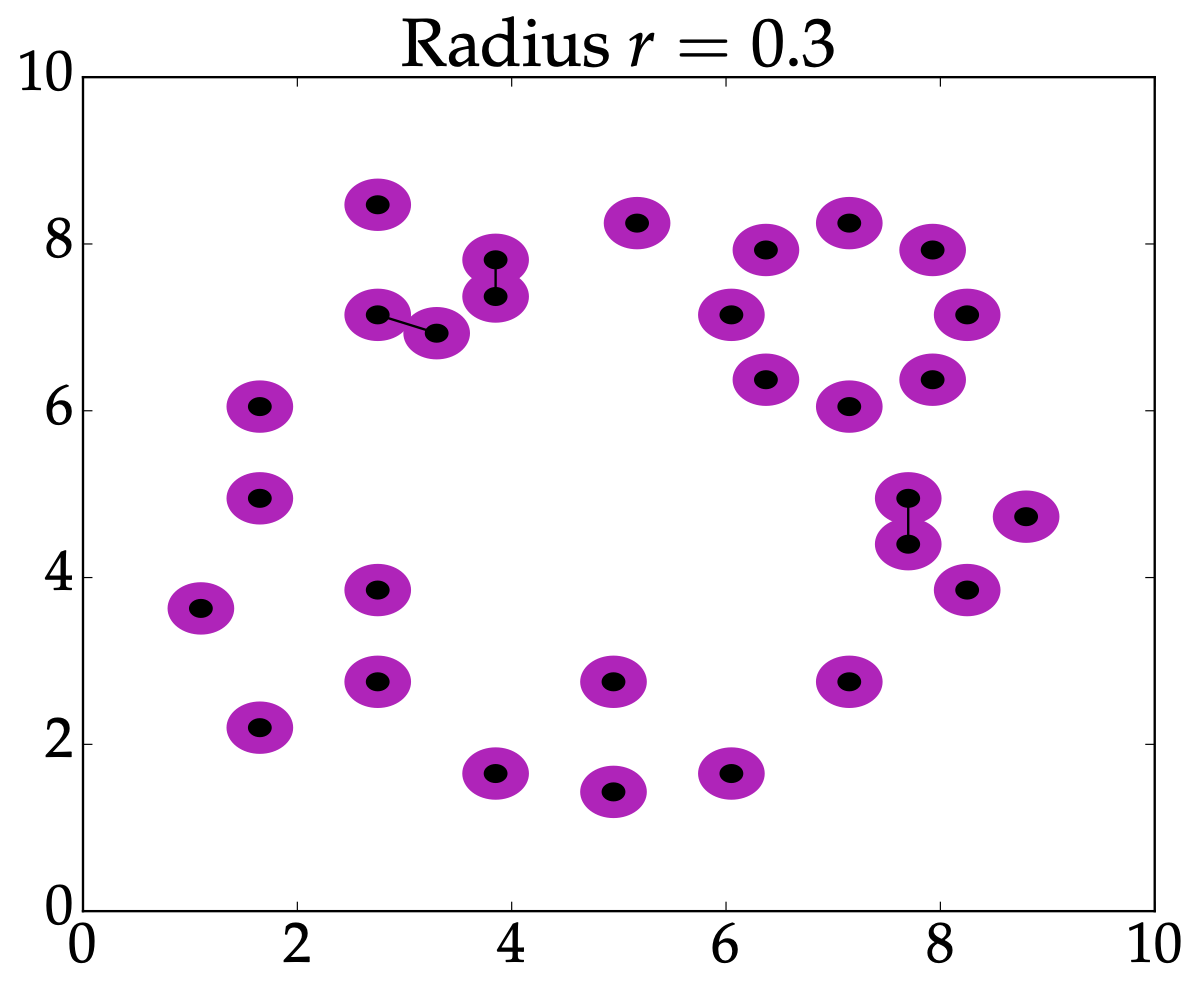
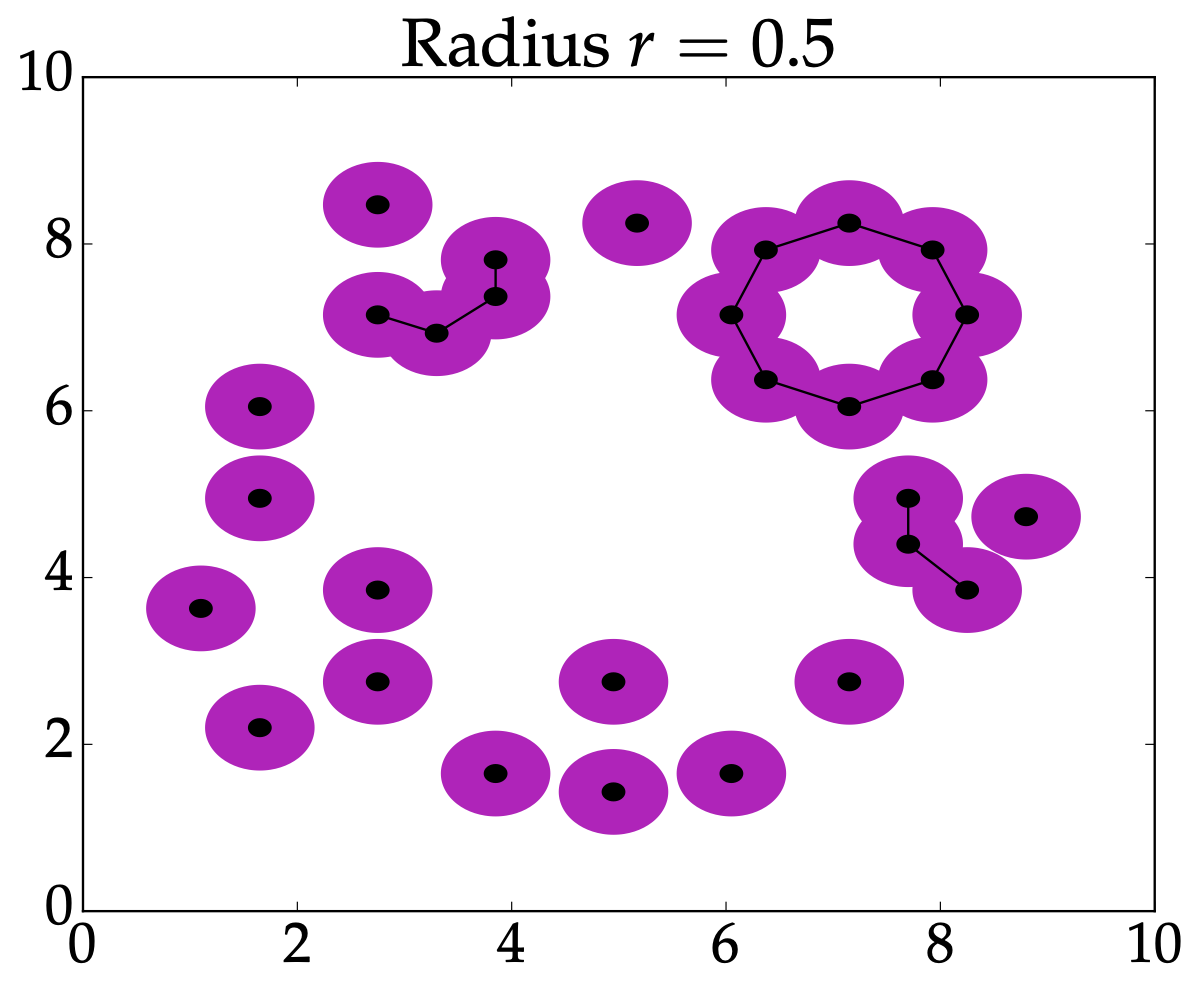
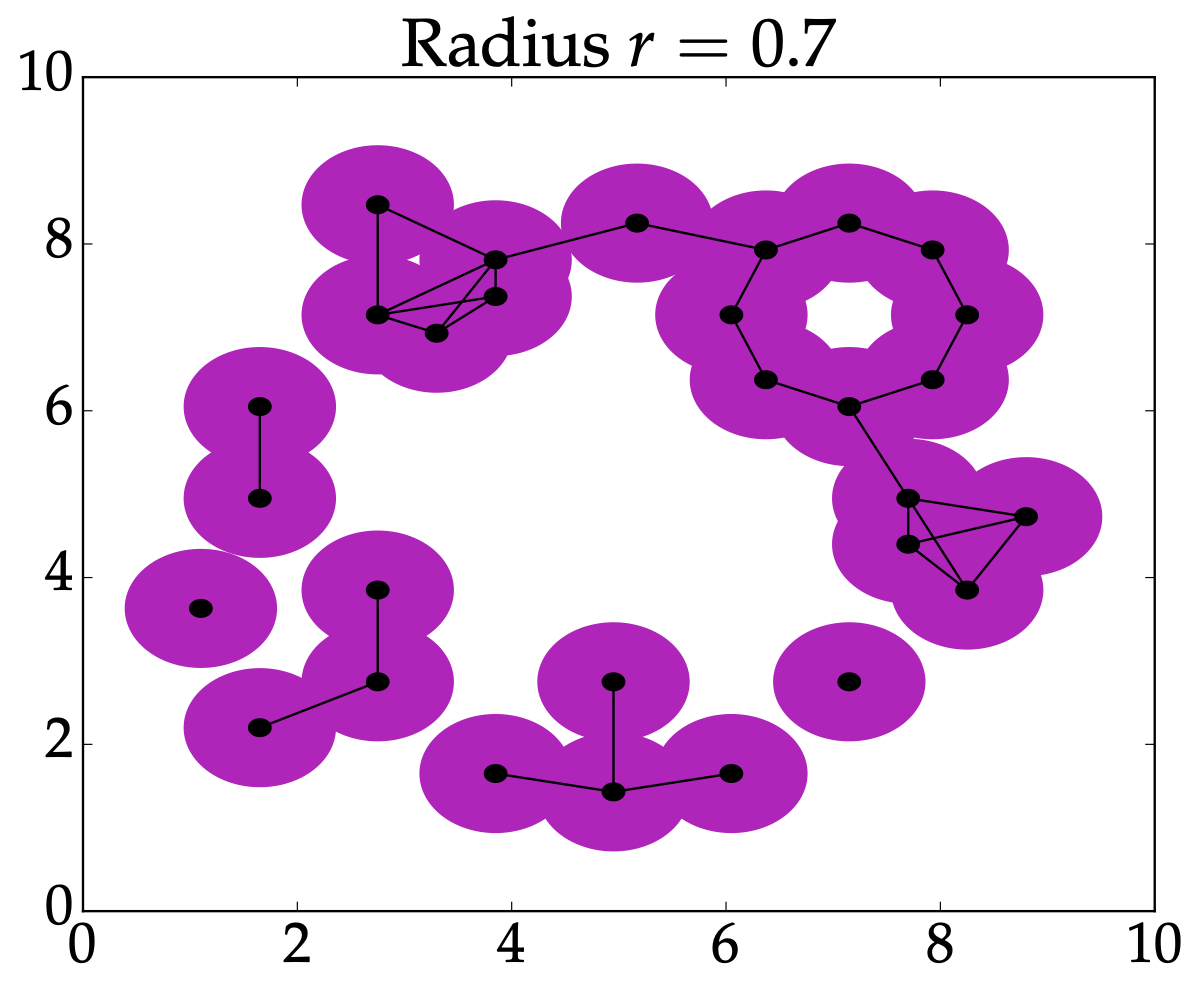
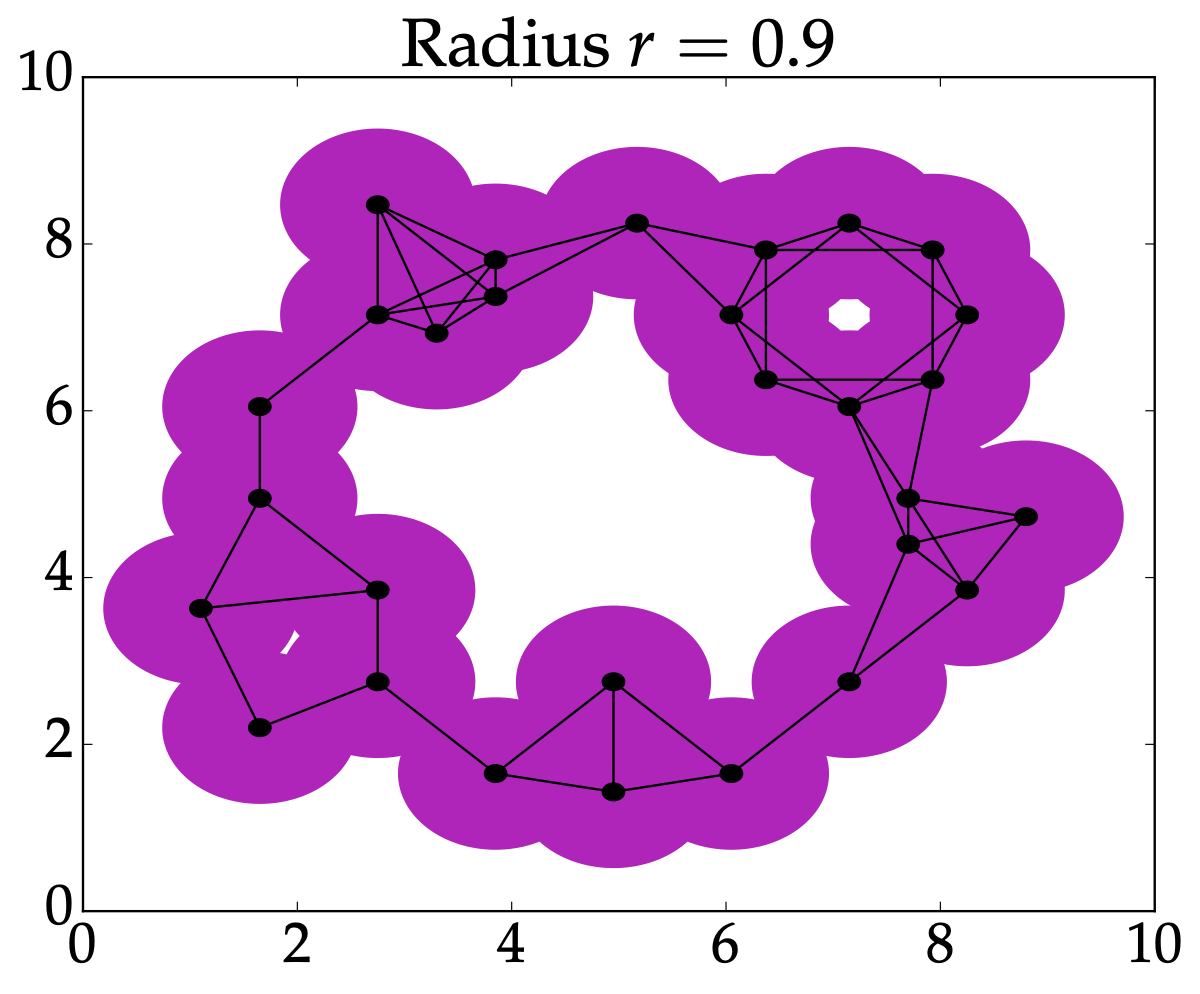
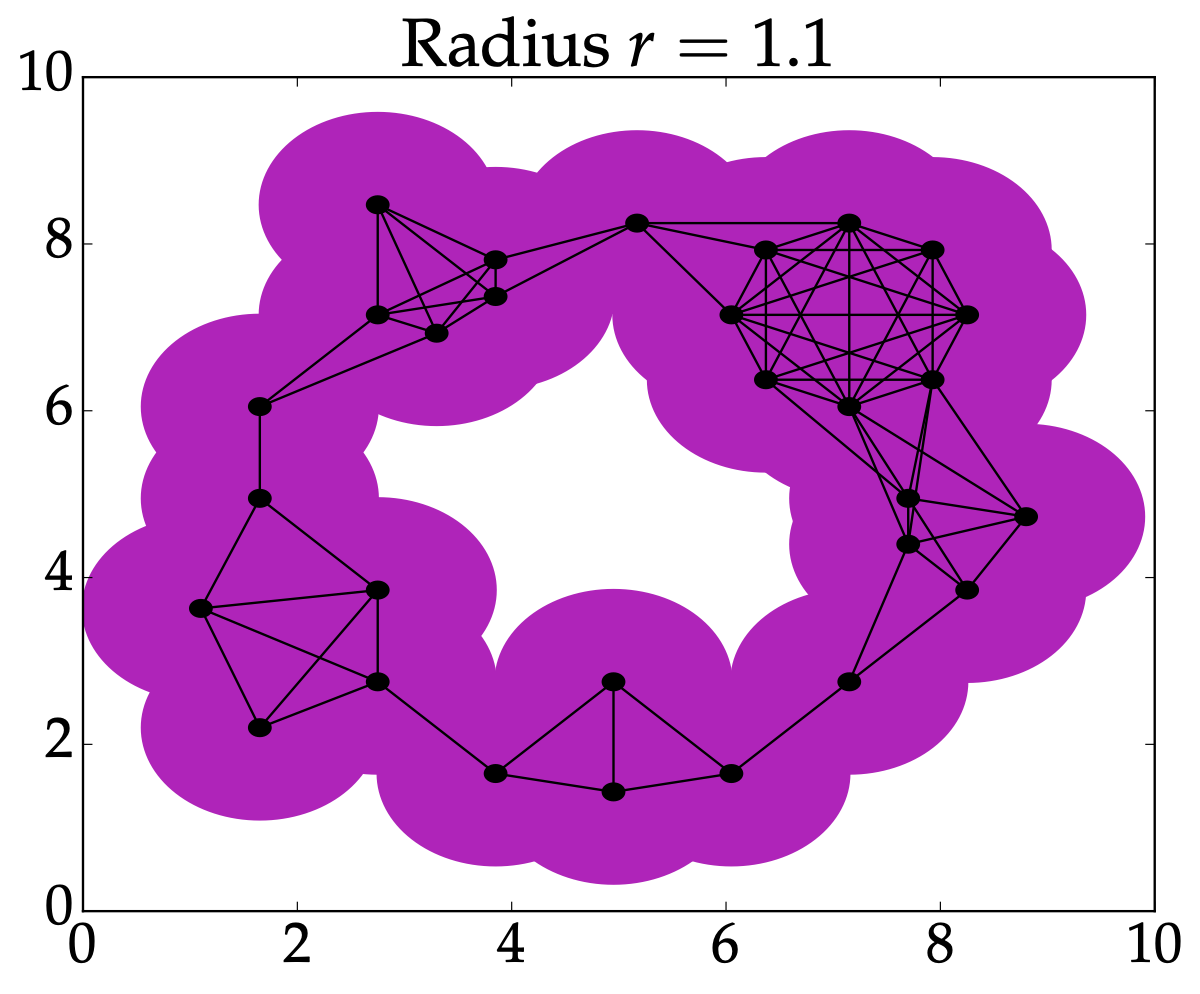
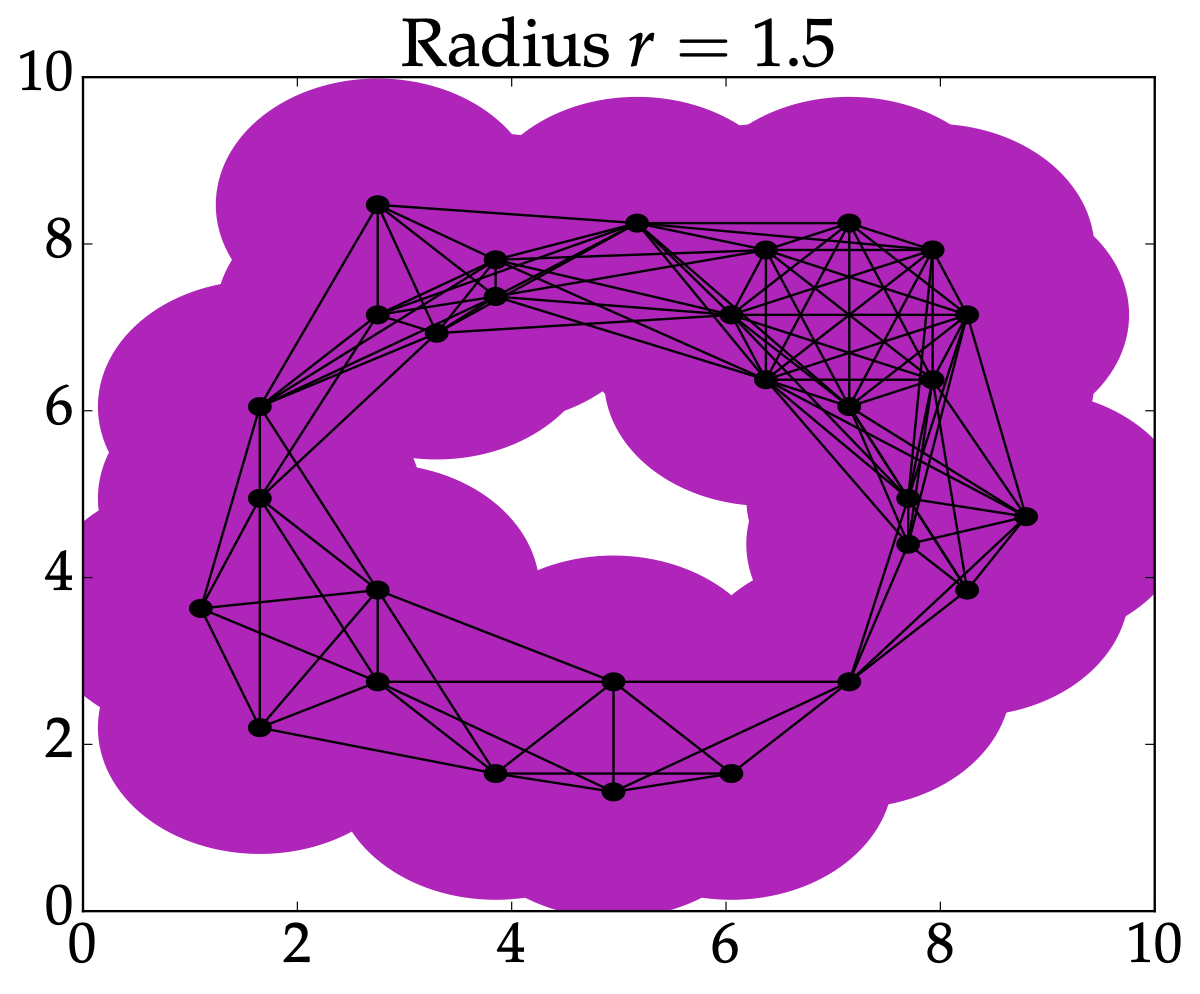
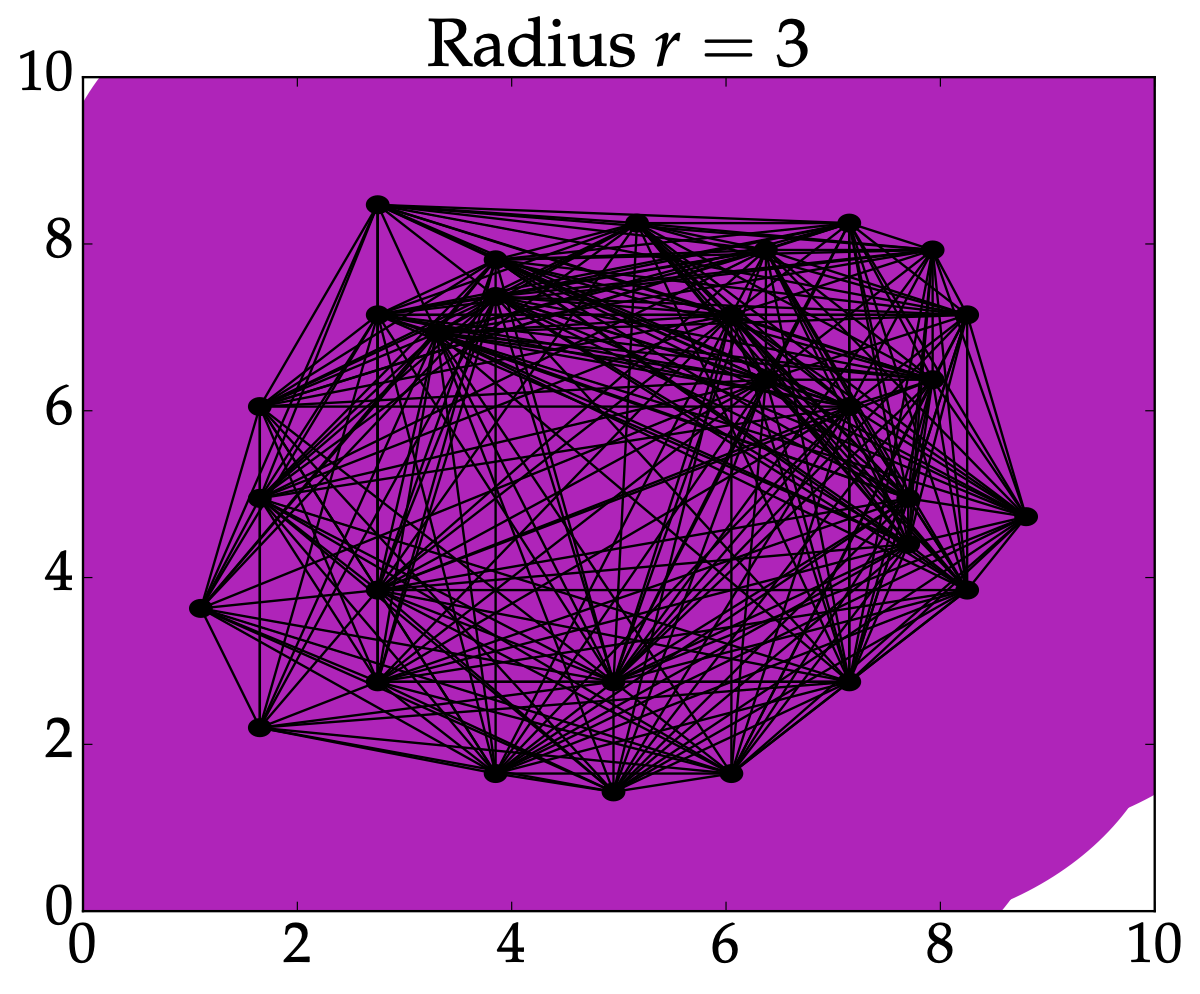
From last time: Nerve

Given a finite collection of sets \(\FF\), the nerve is $$\mathrm{Nrv}(\UU) = {X \subseteq \FF \mid \bigcap _{U \in X} U \neq \emptyset}.

\[ \begin{align}\begin{aligned} From earlier: Homotopy type **Definition:** Two topological spaces $T$ and $U$ are homotopy equivalent if there exist maps $g : T \to U$ and $h : U \to T$ such that $h \circ g$ and $g \circ h$ are homotopic to the appropriate identity maps. - *Intuition*: Can deform one space into the other.\\- Example: Divide the alphabet into *equivalence classes*: collections of letters that are all homotopy equivalent to every other letter in their collection. ::: center A B C D E F G H I J K L M N O P Q R S T U V W X Y Z *Semi-covered in lecture 2* ## Nerve lemma (Metric space version)\\::: theorem Given a finite cover $\UU$ (open or closed) of a metric space $M$, the underlying space $|N(\UU)|$ is homotopy equivalent to $M$ if every non-empty intersection $\bigcap_{i=0}^kU_{\alpha_i}$ of cover elements is homotopy equivalent to a point (contractible).\\## complex\\**Definition:** Let $P \subset (M,d)$ be a finite point cloud. Fix $r \geq 0$. The complex is $$\begin{aligned} \check{C}^r(P) &= \left \{ \sigma \subseteq P \mid \bigcap_{x \in \sigma} B(x,r) \neq \emptyset \right\}\ & = \mathrm{N}(\{B(x,r)\}_{x \in P}) \end{aligned}\end{aligned}\end{align} \]

Example: Cech complex

Warning

The complex is an abstract simplicial complex. The obvious map into \(\mathbb{R}^N\) doesn’t necessarily get you a geometric simplicial complex!

Rips complex

Definition: Given \(P \subseteq (M,d)\), the Vietoris-Rips complex is $$VR^r(P) = \left{ \sigma \subseteq P \mid d(x_i,x_j)\leq 2r \text{ for all } x_i,x_j \in \sigma \right}

\[ \begin{align}\begin{aligned}## Example: Rips complex\\ ## Equilateral triangle example\\ ## Rips-Lemma\\::: theorem Given point cloud $P \subset (M,d)$ and $r \geq 0$, $$\check{C}^r(P) \subseteq VR^r(P) \subseteq \check{C}^{2r}(P) % VR(2r) \subseteq \check{C}(\sqrt{2}r) \subseteq VR(2\sqrt{2}r)\end{aligned}\end{align} \]

Warning: Radius vs diameter

\[ \begin{align}\begin{aligned}VR^r(P) = \left\{ \sigma \subseteq P \mid d(x_i,x_j)\leq 2r \text{ for all } x_i,x_j \in \sigma \right\}\\$$  ## What we want to study\\   \\   # Alpha complex\\## Voronoi diagram\\Given a point cloud $P\subseteq \mathbb{R}^N$. The Voronoi cell of $u \in P$ is $$V_u = \{x \in \mathbb{R}^d \mid \|x-u\| \leq \|x-v\|, v \in P\}\\$$ The Voronoi diagram is the collection of Voronoi cells $Vor(P) = \{V_u \mid u \in P\}$. ## Simple examples ## Website\\<http://alexbeutel.com/webgl/voronoi.html>\\ ## Delaunay triangulation\\The Delaunay complex of point cloud $P \subseteq \mathbb{R}^N$ is the nerve of the Voronoi diagram. $$\mathrm{Del}(P) = \{ \sigma \subseteq P \mid \bigcap _{u \in P} V_u \neq \emptyset\}.\end{aligned}\end{align} \]

Example

Properties

• Delaunay is an abstract simplicial complex.

• If we have points in general position, the obvious embedding gives a geometric simplicial complex.

• Delaunay is FIXED (has nothing to do with a radius or diameter parameter….)

Leading up to the alpha complex

Alpha complex

\(\mathrm{Del}_p^\alpha = \{x \in B(p, \alpha) \mid d (x, p) \leq d (x, q) \text{ for all } q \in P\} = B(p,r) \cap V_p\)

The alpha complex for point cloud \(P\) with radius \(r \geq 0\) is the nerve $$\mathrm{Del}_p^\alpha = \mathrm{Nrv}({D_p^\alpha \mid p \in P}).

$$

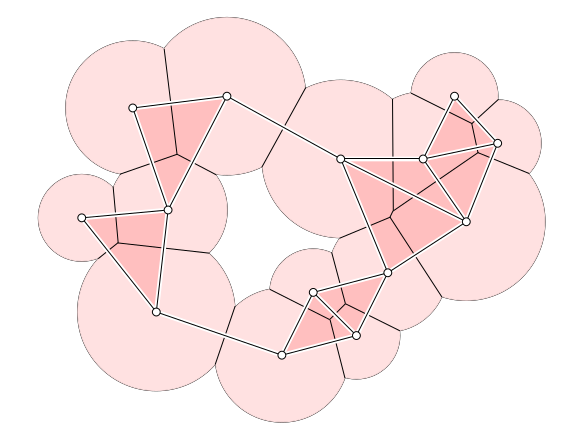
Properties

• \(\mathrm{Alpha}(r) \subseteq \mathrm{Delaunay}\)

• \(\mathrm{Alpha}(r) \subseteq \check{C}(r)\)

• \(\mathrm{Alpha}(r)\) has the same homotopy type as the union of balls of radius \(r\). For next time

• EH III.7 (p75) Let \(P \subseteq \mathbb{R}^d\) be a finite set of points in general position. Denote by \(\check{C}(r)\) and \(\mathrm{Alpha}(r)\) as the and alpha complexes for radius \(r \geq 0\), respectively.

  Is it true that \(\mathrm{Alpha}(r) = \check{C}(r) \cap \mathrm{Delaunay}\)?

  If yes, prove the following two subcomplex relations. If no, give examples to show which subcomplex relations are not valid.

  1. \(\mathrm{Alpha}(r) \subseteq \check{C}(r) \cap \mathrm{Delaunay}.\)

  2. \(\check{C}(r) \cap \mathrm{Delaunay} \subseteq \mathrm{Alpha}(r)\)