Slide transcript

Slide transcript#

I am working on finding ways to increase accessibility of the beamer slides provided. The following is an automatically generated transcript from the pdf of the slides but is still not perfect. I would be happy to hear feedback on how this transcript can be improved for additional usefulness.

Lecture 3 - Simplicial Complexes#

Goals#

Goals for today: Ch 2.1

Define geometric/abstract simplicial complexes
Define simplicial maps

Idea#

A simplicial complex is a generalizion of a graph

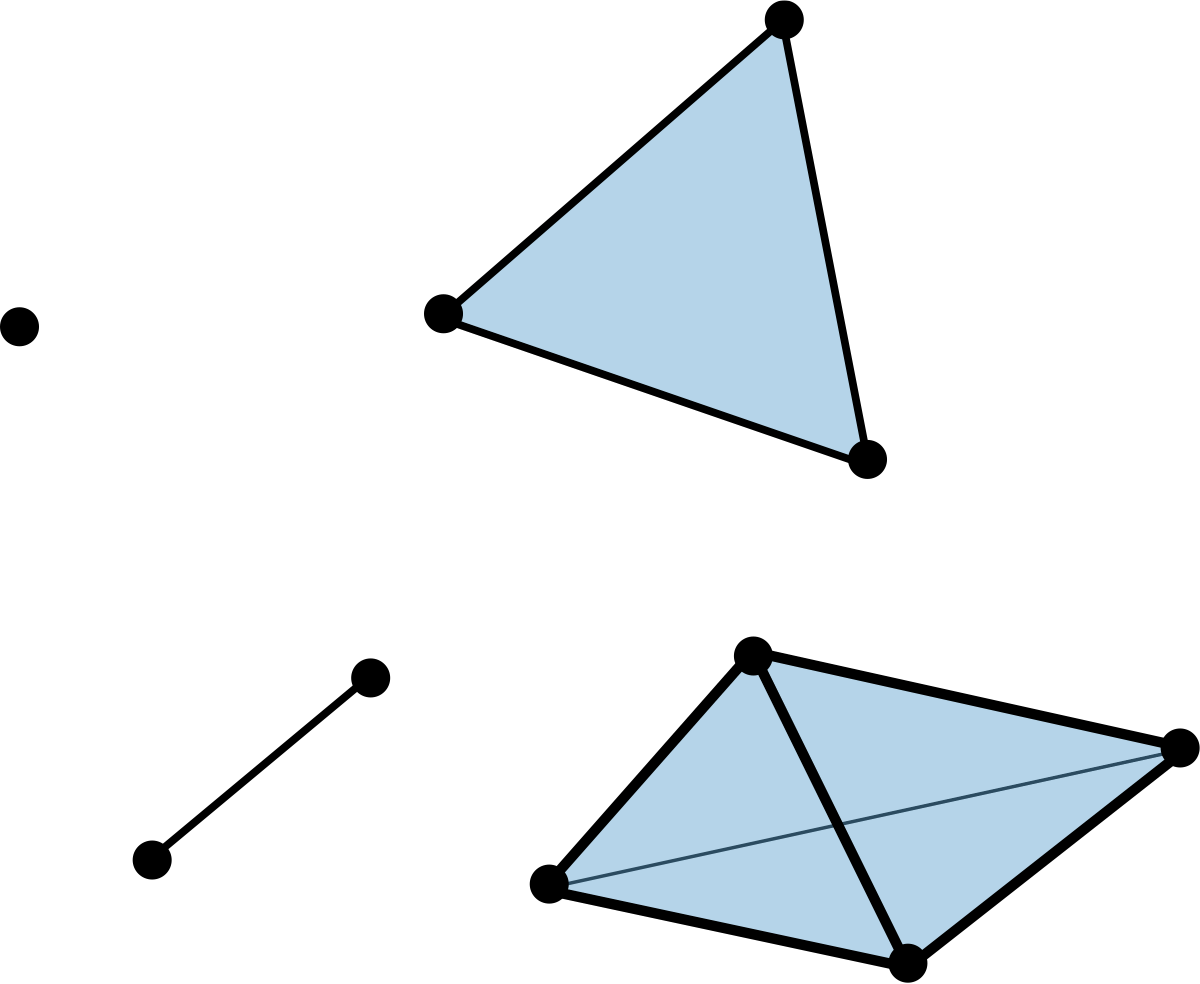
General position#

A set $\{a_0,\cdots,a_n\} \subset \mathbb{R}^N$ is in general position if no $k$ of them lie in a $k-2$ dimensional hyperplane ($k = 2,3,\ldots,N+1$).

Warning: Papers will often modify this definition to suit their purposes!

$n$-Plane#

Given a set of points $\{a_0,\cdots,a_n\}$ in general position, the $n$-plane $P$ spanned by the points is $$P = \left{\sum_{i=0}^n t_i a_i \in \mathbb{R}^N \mid \sum t_i = 1\right}.

\[ \begin{align}\begin{aligned} ## $n$-simplex\\Given a set of points $\{a_0,\cdots,a_n\}$ in general position, the $n$-simplex $\sigma$ spanned by the points is $$P = \left\{\sum_{i=0}^n t_i a_i \in \mathbb{R}^N \mid \sum t_i = 1\right\}\end{aligned}\end{align} \]

such that $t_i \geq 0$ $\forall i$.

Barycentric coordinates#

The numbers $t_i$ are uniquely determined by $x$ and are called barycentric coordinates.

More definitions#

$\{a_0,\cdots,a_n\}$ are called the vertices of $\sigma$.
The dimension of $\sigma = [a_0,\cdots,a_n]$ is $n$.
Any simplex spanned by a subset of $\{a_0,\cdots,a_n\}$ is a face of $\sigma$.
A face is proper if it isn’t the simplex itself.

Even more definitions#

The union of the proper faces is the boundary of $\sigma$, $\mathrm{Bd}(\sigma)$.
The interior of $\sigma$ is $\sigma - \mathrm{Bd}(\sigma)$. This is sometimes called the open simplex.

Geometric simplicial complex#

A (geometric) simplicial complex $K$ in $\mathbb{R}^N$ is a (finite) collection of simplices in $\mathbb{R}^N$ such that

Every face of a simplex of $K$ is in $K$.
The intersection of any two simplices of $K$ is a face of each.

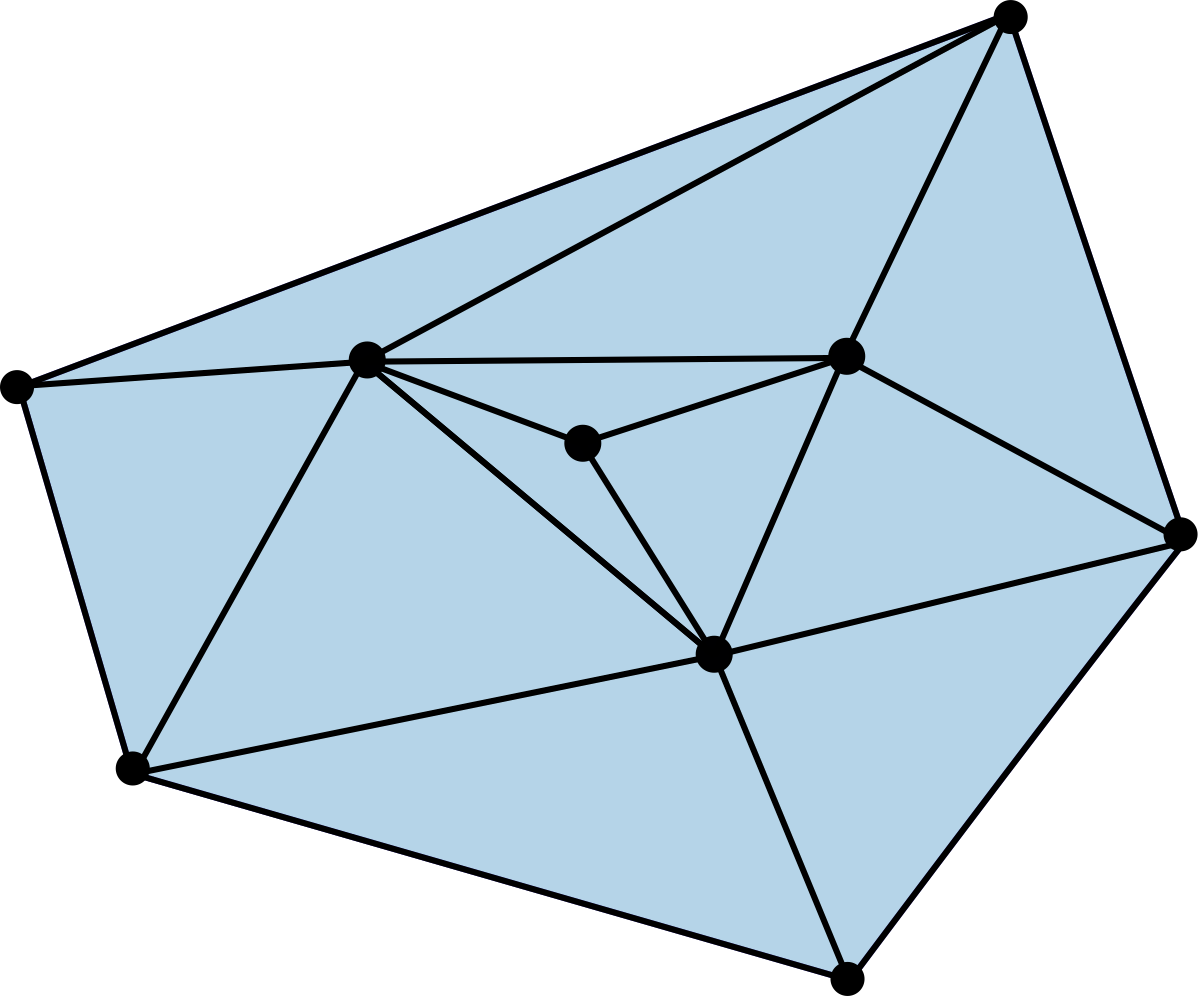
Dimension#

The dimension of $K$ is the maximum dimension of its simplices.

Abstract simplicial complexes#

An abstract simplicial complex $\mathcal{K}$ is a (finite) collection of (finite) non-empty sets of $V$ such that $\alpha \in \mathcal{K}$ and $\beta \subseteq \alpha$ implies $\beta \in \mathcal{K}$.

Two types#

Geometric Abstract Geometric realization, underlying space

Subcomplex#

If $L$ is a subcollection of $K$ that contains all faces of its elements, then $L$ is called a subcomplex.

A subcomplex $L \subset K$ is full if it contains all simplices of $K$ spanned by the vertices in $L$.

Skeleton#

The subcomplex of $K$ consisting of all simplices of dimension $\leq p$ is called the $p$-skeleton of $K$, usually denoted $K^p$.

Stars#

The star of a simplex $\sigma \in K$, is the set of simplices that have $\sigma$ as a face: $\mathrm{St}(\sigma) = \{\tau \in K \mid \sigma \leq \tau\}$.

Warning: $\mathrm{St}(\sigma) \subset |K|$ is not a simplicial complex!
The closed star, $\overline{\mathrm{St}}(\sigma)$, is the closure of $\mathrm{St}(\sigma)$.

Links#

The link of a simplex is $\overline{\mathrm{St}}(\sigma) - \mathrm{St}(\sigma).$

Nerve#

Given a finite collection of sets $\FF$, the nerve is $$\mathrm{Nrv}(\UU) = {X \subseteq \FF \mid \bigcap _{U \in X} U \neq \emptyset}.

\[ \begin{align}\begin{aligned}![image](../Figures/Fig2p2)\\## Check: This is actually an abstract simplicial complex!\\Recall: $K$ is a simplicial complex if $\sigma \in K$ and $\tau \leq \sigma$ implies $\tau \in K$. $$\mathrm{Nrv}(\FF) = \{X \subseteq \FF \mid \bigcap _{U \in X} U \neq \emptyset\}.\end{aligned}\end{align} \]

Try it: What is the nerve of this collection of disks?#

Try it: What is the nerve of this collection of sets?#

The difference between the examples#

Homework Pick one

Let $K$ be a simplicial complex. Show that $K$ is the nerve of the collection of stars of its vertices.
A flag in a simplicial complex $K$ is a nested sequence of proper faces $\sigma_0 <\sigma_1<\cdots<\sigma_k$. Show that the collection of flags in $K$ forms a simplicial complex; this is called the order complex of $K$.

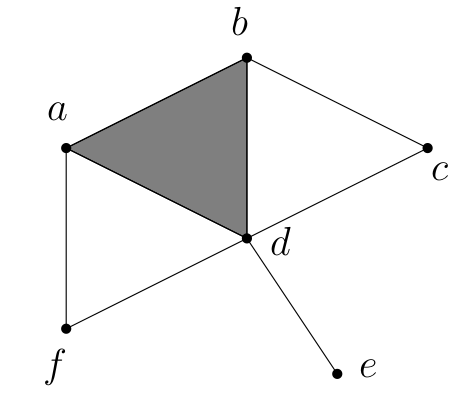
For either question, show the construction on the simplicial complex below.