Slide transcript

Slide transcript#

I am working on finding ways to increase accessibility of the beamer slides provided. The following is an automatically generated transcript from the pdf of the slides but is still not perfect. I would be happy to hear feedback on how this transcript can be improved for additional usefulness.

Lecture 2 - Maps and Morse Function Preliminaries#

Where were we?

  • Basics of topology - open, closed, connected,

  • Maps \(f: A \to B\)

Maps#

Maps

Definition: A function \(f : T \to U\) is continuous if for every open set \(Q \subseteq U\), \(f^{-1} (Q)\) is open. Continuous functions are also called maps. Ex1. \(f:\mathbb{R} \to \mathbb{R}\), \(f(x) = x^2\) Ex2. \(g: \mathbb{R} \to \mathbb{R}\) \(g(x) = \lfloor x \rfloor\) Embedding

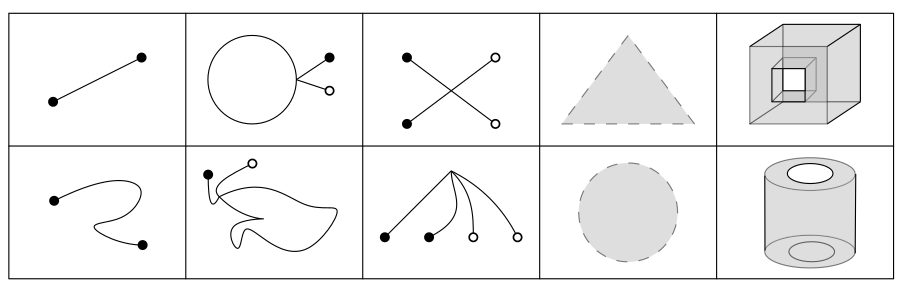
Definition: A map \(g : T \to U\) is an embedding of T into U if g is injective.

Injective (1-1): \(f(x) = f(y)\) iff \(x=y\) Ex1. \(f:\mathbb{R} \to \mathbb{R}\), \(f(x) = x^3\) Ex2. \(g: \mathbb{S}^1 \to \mathbb{R}^2\) Homeomorphism

Definition: Let \(T\) and \(U\) be topological spaces.

A homeomorphism is a bijective map \(h : T \to U\) whose inverse is also continuous.

Two topological spaces are homeomorphic if there exists a homeomorphism between them. image Homeomorphism: Cheap trick

If \(T\) and \(U\) are compact metric spaces, every bijective map from \(T\) to \(U\) has a continuous inverse.

Homotopy

Definition: Let \(g : X \to U\) and \(h : X \to U\) be maps.

A homotopy is a map \(H : X \times [0, 1] \to U\) such that \(H(\cdot, 0) = g\) and \(H(\cdot, 1) = h\).

Two maps are homotopic if there is a homotopy connecting them.

Annulus example - Homotopy Annulus: \(A = \{ (\theta,r) \mid 1 \leq r \leq 2\}\). Circle: \(\mathbb{S}^1 = \{ (\theta,r) \mid r = 1\}\) \(g : A \to A\) identity. \(h : A \to A\), \(h(\theta,r) = (\theta,1)\). Show \(R(\theta, r, t) = (\theta,(1-t)r+t)\) is a homotopy. Homotopy equivalent

Definition: Two topological spaces \(T\) and \(U\) are homotopy equivalent if there exist maps \(g : T \to U\) and \(h : U \to T\) such that \(h \circ g\) and \(g \circ h\) are homotopic to the appropriate identity maps.

Annulus example - Homotopy equivalent Show \(A\) is homotopy equivalent to \(\mathbb{S}^1 \subset A\) Retract

Definition: Let \(T\) be a topological space, and let \(U \subset T\) be a subspace.

A retraction \(r\) of \(T\) to \(U\) is a map \(r:T \to U\) such that \(r(x) = x\) for every \(x \in U\). Ex: Annulus to circle Deformation retract

Definition: The space \(U \subseteq T\) is a deformation retract of \(T\) if the identity map on \(T\) can be continuously deformed to a retraction with no motion of the points already in \(U\).

Specifically, there is a homotopy \(R : T \times [0, 1] \to T\) such that

  • \(R(\cdot, 0)\) is the identity map on \(T\),

  • \(R(\cdot, 1)\) is a retraction of \(T\) to \(U\), and

  • \(R(x, t) = x\) for every \(x \in U\) and every \(t \in [0, 1]\).

Annulus example: Deformation retract \(R(\theta, r, t) = (\theta,(1-t)r+t)\).

Check that \(R\) satisfies the three properties to be a deformation retract. Why do I care?

If \(U\) is a deformation retract of \(T\), then \(T\) and \(U\) are homotopy equivalent. Ex. 1 image

Ex.2 A to O TRY IT: Alphabet Divide the alphabet into equivalence classes: collections of letters that are all homotopy equivalent to every other letter in their collection.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Manifolds

Manifold definition

Definition: A topological space \(M\) is an \(m\)-manifold if every point \(x \in M\) has a point homeomorphic to the \(m\)-ball \(\mathbb{B}_o^d\) or the \(m\)-hemisphere \(\mathbb{HQ}^d\). \(\mathbb{B}_o^d = \{ y \in \mathbb{R}^{d} \mid \|y\| < 1\) \(\mathbb{HQ}^d = \{y \in \mathbb{R}^d \mid d(y,0)<1 \text{ and } y_d \geq 0\}\).

image More manifold vocab

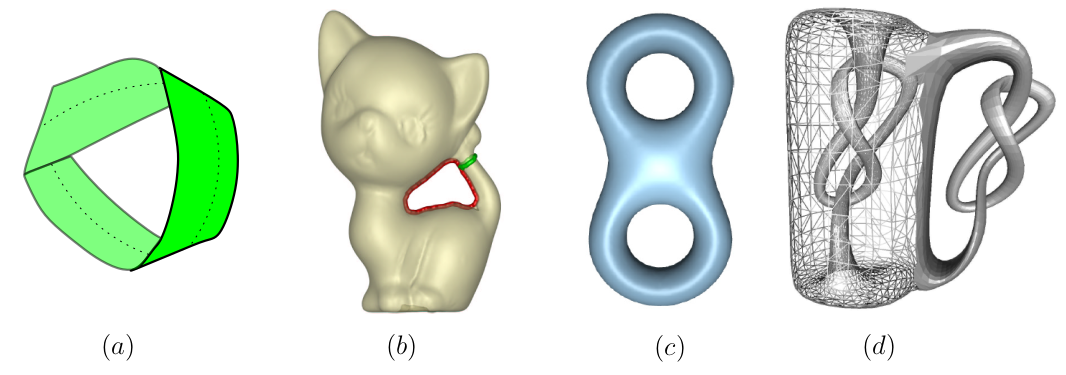
  • Manifold with/without boundary

  • Surface: 2-manifold subspace of \(\mathbb{R}^d\)

  • Non-orientable: can start at point \(p\), stand on one side of the manifold and walk back to \(p\) but be on the other side

  • Loop: 1-manifold without boundary

  • Genus: of a surface is \(g\) if \(2g\) is the maximum number of loops that can be removed without disconnecting the surface.

  • Smooth embedded manifold: No wrinkles, no zero directional derivative Gradients

Definition: Given a smooth function \(f:\mathbb{R}^d \to \mathbb{R}\), the gradient vector field \(\nabla f:\mathbb{R}^d \to \mathbb{R}^d\) at \(x\) is: $$\nabla f (x) = \left[ \frac{\partial f}{\partial x_1}(x), \cdots, \frac{\partial f}{\partial x_d}(x) \right]

\[ \begin{align}\begin{aligned}*Note: This definition can be extended to more general settings $f:M \to \mathbb{R}$.* Ex. $f:\mathbb{R}^2 \to \mathbb{R}$, $f(x_1,x_2) = x^2+y^2$ at $(0,0)$ and $(1,0)$ Critical points\\- Points in $\mathbb{R}^d$ where $\nabla f(p) = [0,\cdots,0]$\\![image](../Figures/Fig1p9.png) "Nice" critical points\\**Definition:** For a smooth $m$-manifold $M$, the Hessian matrix of $f:M \to \mathbb{R}$ is the matrix of second order partial derivatives\\![image](../Figures/Def1p27.png)\\A critical point of $f$ is non-degenerate if the Hessian is non-singular (has non-zero determinant); otherwise it is degenerate.\\TRY IT: Saddle Ex. $f:\mathbb{R}^2 \to \mathbb{R}$, $f(x,y) = x^2 - y^2$. Is the critical point at the origin degenerate?\\Interactive plot: <https://www.desmos.com/3d/cw0km8przc> TRY IT: Monkey saddle Ex. $f:\mathbb{R}^2 \to \mathbb{R}$, $f(x,y) = x^3 - 3xy^2$. Is the critical point at the origin degenerate?\\Interactive plot: <https://www.desmos.com/3d/cw0km8przc> Morse lemma\\::: theorem Given a smooth function $f: M \to \mathbb{R}$ defined on a smooth $m$-manifold $M$, let $p$ be a non-degenerate critical point of $f$.\\There is a local coordinate system in a neighborhood $U(p)$ so that\\- $U(p) = (0,\cdots,0)$\\- Locally any $x$ is of the form $$f(x) = f(p) - x_1^2 - \cdots - x_s^2 + x_{s+1}^2 + \cdots + x_m^2.\end{aligned}\end{align} \]

In this case, the integer \(s\) is called the index of the critical point \(p\).

Back to critical points 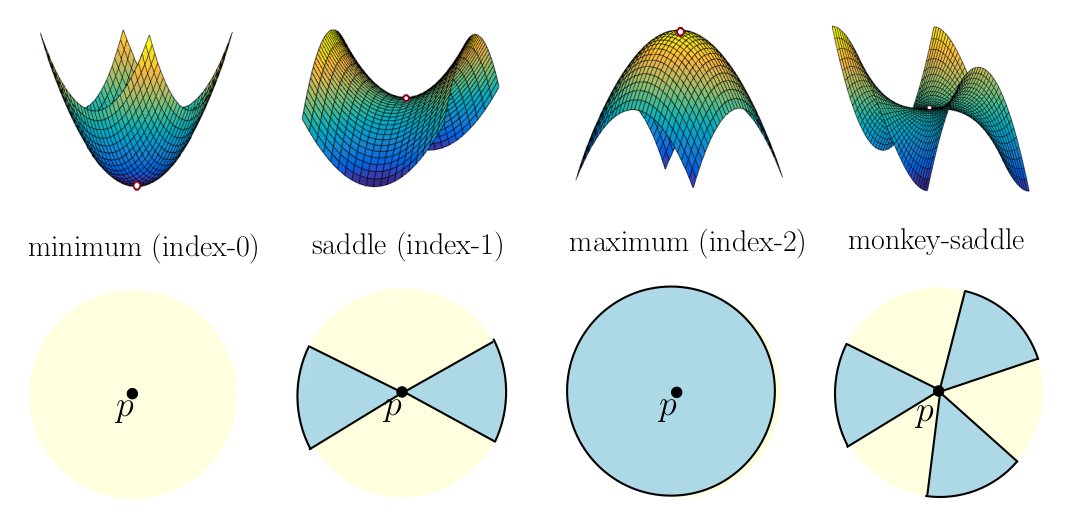image Morse Functions

Definition: A smooth function \(f:M \to \mathbb{R}\) defined on a smooth manifold \(M\) is a Morse function if

  • none of \(f\)’s critical points are degenerate

  • the critical points have distinct function values. Why do I care? Every function is almost Morse. Morse Functions and sublevelsets

image Homework for next time

Choose one of the following to present.

  1. DW 1.6.9

  2. DW 1.6.10

  3. DW 1.6.12

Contents