Slide transcript

Slide transcript#

I am working on finding ways to increase accessibility of the beamer slides provided. The following is an automatically generated transcript from the pdf of the slides but is still not perfect. I would be happy to hear feedback on how this transcript can be improved for additional usefulness.

Lecture 1 - Introduction & Topology Basics#

Syllabus#

  • Available on the course website: elizabethmunch.com/cmse890

  • Schedule & Office hours

  • Slack

  • Prerequisites:

    • Linear Algebra

    • Some programming experience

  • Python, jupyterhub, and engineering DECS accounts

  • Homework

    • Present a problem assigned in the previous class

    • Approximately twice during the semester

    • Goal: Present on something not in your expertise

Textbook#

image Introductions

  • Name

  • Department/Program

  • Research interest

  • Non-work interest

Topological Data Analysis#

Shape in data#

image

image

image

image

image

image

Images: Wikipedia, Szymczak et al., Ma et al.

<1-2>

Topological Data Analysis (TDA)#

image Raw Data X-ray CT Point Clouds Networks Topological Summary Persistence Diagrams Euler Characteristic Curves Mapper graphs

Analysis Statistics Machine Learning

What is topology?#

Topology \(\neq\) Topography Mathematical study of spaces preserved under continuous deformations

  • stretching and bending

  • not tearing or gluing

image

Study of the shape and features of the surface of the Earth

image Images: Wikipedia

History Pt 2#

  • Esoteric field of study 1700-2000

    • Algebraic topology

    • Applications/intersections with dynamical systems

    • Would never be considered “applied” in traditional sense.

    Topology, the pinnacle of human thought. In four centuries it may be useful.

    • Alexander Solzhenitzin, “The First Circle” 1968

  • Things change ca.2000

    • Introduction of Persistent Homology

History#

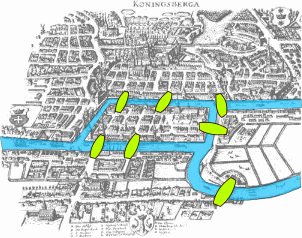
image Leonhard Euler (1707-1783)

image image image

Bridges of Konigsberg

Images: Wikipedia <2>

Topological Invariants- Euler Characteristic#

Images: Wikipedia

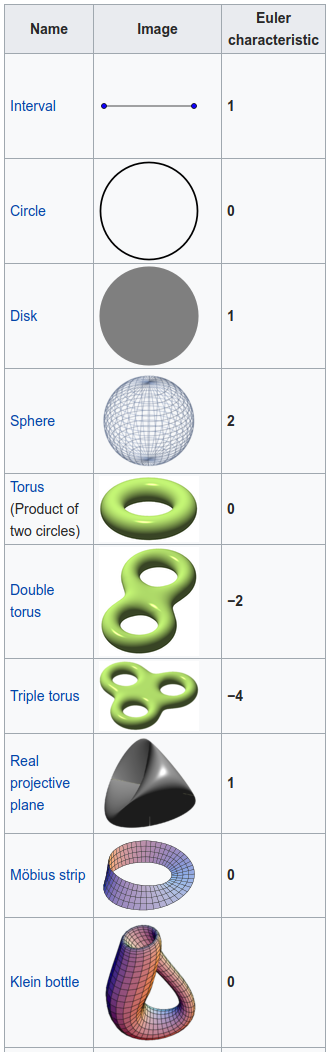Euler characteristic as topological signature image Different Euler characteristics mean spaces must be topologically different

Different spaces might have the same Euler characteristics Euler characteristic is an example of a topological signature

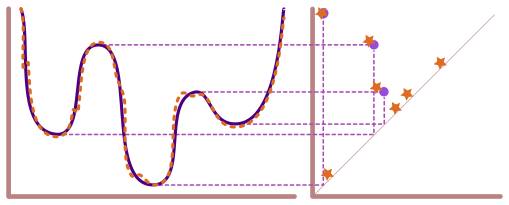
Quantification vs Representation of Shape#

image Persistent Homology

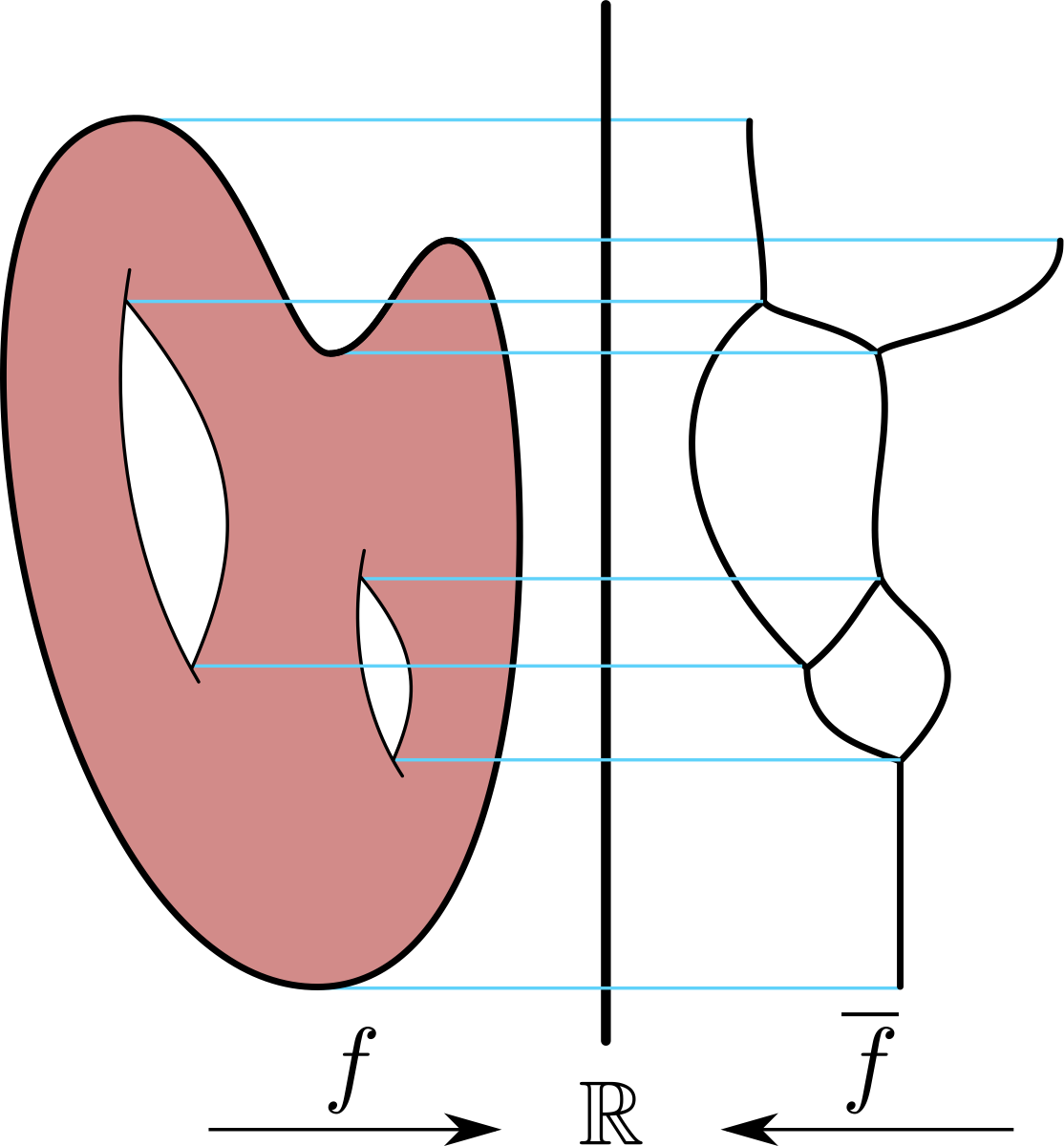image Reeb graph

image

Mapper

Current active research directions#

  • Multidimensional persistence

  • Machine learning, statistics

  • Time series analysis and dynamical systems

  • Metrics

  • Parallelization

  • Visualization

  • Application areas:

    • Neuroscience

    • Plant Biology

    • Gene expression

    • Image processing

    • Sensor networks

    • Atmospheric science

Goals for this course#

  • Understand the computation and interpretation of several commonly used tools in TDA

    • Persistent Homology

    • Reeb graphs

    • Mapper

  • Know what types of data and/or are amenable to TDA methods.

  • Have experience working with open-source code banks for computation.

Intro to Topology Vocabulary#

Goals of this section#

  • Cover some basic terms from Ch 1.1, 1.2, 1.3

  • Depending on your math background, this might be obvious or this might seem impossible. If the latter, spend some time tonight trying some examples! Oh yeah, and read the textbook!

Topology#

Definition: A topological space is a point set \(\mathbb T\) with a set of subsets \(T\) (called open sets) such that

  • \(\emptyset\), \(\mathbb T\) \(\in T\)

  • For every \(U \subseteq T\), the union of the sets in \(U\) is in \(T\)

  • For every finite \(U \subseteq T\), the common intersection of the subsets in \(U\) is in \(T\). Ex. \(\mathbb T= \{a,b,c\}\), \(T = \{ \emptyset, T_1 = \{a\}, T_2 = \{b\}, T_3 = \{a,b\}, \mathbb T= \{a,b,c\} \}\)

Metric - \(L_2\)#

Definition: A metric space is a pair \((\mathbb T,d)\) where \(\mathbb T\) is a set, and \(d: \mathbb T\times \mathbb T\to \mathbb R\) satisfies

  • \(d(p,q) = 0\) iff \(p=q\)

  • \(d(p,q) = d(q,p)\) for all \(p,q \in \mathbb T\)

  • \(d(p,q) \leq d(p,r) + d(r,q)\) for all \(p,q,r \in \mathbb T\) Example: \(\mathbb T= \mathbb R^2\), \(d((a,b), (c,d)) = \sqrt{(c-a)^2 + (b-d)^2}\)

Metric - \(L_\infty\)#

Definition: A metric space is a pair \((\mathbb T,d)\) where \(\mathbb T\) is a set, and \(d: \mathbb T\times \mathbb T\to \mathbb R\) satisfies

  • \(d(p,q) = 0\) iff \(p=q\)

  • \(d(p,q) = d(q,p)\) for all \(p,q \in \mathbb T\)

  • \(d(p,q) \leq d(p,r) + d(r,q)\) for all \(p,q,r \in \mathbb T\) Example: \(\mathbb T= \mathbb R^2\), \(d((a,b), (c,d)) = \max \{|u_1-v_1| , |u_2-v_2|\}\)

Metric Topology#

Definition: Given a metric space \((\mathbb T,d)\), an open metric ball is

\[B_o(c,r) = \{ p \in \mathbb T\mid d(p,c) < r\}.\]

The metric topology is the set of all metric balls

\[\{ B_o(c,r) \mid c \in \mathbb T, 0 < r \leq \infty\}.\]

Ex. \(\mathbb R\), \(\mathbb R^2\) TRY IT: Draw the subset of \(\mathbb R^2\) contained in \(B_o(0,1)\) for \(d((u_1,u_2),(v_1,v_2)) =\)

  • \(\| u-v \|_1 = |u_1-v_1| + |u_2-v_2|\)

  • \(\| u-v \|_2 = \sqrt{(u_1-v_1)^2 + (u_2-v_2)^2}\)

  • \(\| u-v \|_\infty = \max \{|u_1-v_1| , |u_2-v_2|\}\) Open and closed sets

Definition: A set is open if it is in the topology \(T\). A set is closed if its complement is open. Ex 1. \(\mathbb T= \{a,b,c\}\), \(T = \{ \emptyset, T_1 = \{a\}, T_2 = \{b\}, T_3 = \{a,b\}, \mathbb T= \{a,b,c\} \}\)

Open and closed sets - metric space version

Limit points#

Definition: Let \(Q \subset \mathbb T\) be a point set. A point \(p \in \mathbb T\) is a limit point of \(Q\) if for every \(\varepsilon>0\), \(Q\) contains a point \(q \neq p\) with \(d(p,q) <\varepsilon\).

Open and closed sets - metric space version

Definition:

  • \(\mathrm{Cl}(Q)\): The closure of a point set \(Q \subseteq \mathbb T\) is the set containing every point in Q and every limit point of \(Q\).

  • A point set \(Q\) is closed if \(Q = \mathrm{Cl} (Q)\), i.e. \(Q\) contains all its limit points.

Open and closed sets - metric space version

Complement version#

Definition:

  • The complement of a point set \(Q\) is \(T \setminus Q\).

  • A point set \(Q\) is open if its complement is closed, i.e. \(T \ Q = \mathrm{Cl} (T \setminus Q)\).

Open cover

Definition: An open (closed) cover of a topological space \((\mathbb T, T )\) is a collection \(C\) of open (closed) sets so that \(T \subseteq \bigcup_{U \in C}\). Ex. \(\mathbb R\), \(C = \{ (n-1,n+1) \mid n \in \mathbb Z\}\) Connected

Definition: A topological space \((\mathbb T, T )\) is disconnected if there are two disjoint non-empty open sets \(U, V \in T\) so that \(T = U \cup V\). A topological space is connected if its not disconnected. Ex. \(A = (1,2) \cup (5,7) \subset \mathbb R\)

Maps#

Homework for next time

Need a volunteer! For this homework, it can’t be someone who is a Math PhD student, preferably someone who hasn’t taken a topology class.

Choose two of the following to present.

  1. DW 1.6.1. Be sure to explain why the constructions you have created are/are not Hausdorff.

  2. DW 1.6.2

  3. DW 1.6.3

  4. DW 1.6.4

  5. DW 1.6.5

  6. DW 1.6.6

Contents